论作品独创性的定量分析

作者 | 杨敏锋  北京君策知识产权发展中心研究室主任

（本文系知产力获得独家首发的稿件，转载须征得作者本人同意，并在显要位置注明文章来源。）

（本文5144字，阅读约需10分钟）

备  注：

本文为作者对在先发表的论文进行通俗化和趣味化改写而成，原文可见杨敏锋：《论作品独创性的数学计算模型》，《知识产权》2018年第8期。

摘  要

作品可看作由多个独立的意思表达单元“元素”组成的集合，其独创性等于该集合中元素排列组合数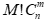（）与各元素的表达方式连续相乘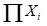（）的积（）。

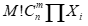关键词

独创性、定量分析、数学模型

一、独创性的定量分析

 在著作权制度中，“独创性”无疑是一个极为重要而又难以精确判断的概念。独创性是获得著作权保护的必要条件，缺乏独创性会被排除在保护范围之外。顾名思义，独创性包含了“独立创作、源于本人”和含有“一定水准的智力创造高度”[1]两个要件。不过，《著作权法》及其实施条例以及相关司法解释，都没有对“独创性”的判断标准作出明确界定。在独创性的分析中，理论上应当涉及到两个问题，即有没有独创性，以及独创性到底有多少。前一个问题涉及的是定性问题，而后一个问题则涉及的是定量问题。

在日常生活中，我们对定性和定量问题的探讨极为常见。如恋爱中的年轻女孩，往往都会问男友两个问题：“你爱我吗”以及“你会爱我多久”？前一个问题属于对“爱”的定性讨论，理论上有肯定和否定两种回答，但实际上明显只有一种。后一个问题则是定量判断，需要给出一个确切的数值，如“一千年”“一万年”“海枯石烂”之类。——按照目前人类的预期寿命，这点其实也无法做到。

在著作权司法实践中，法院认可独创性有高低之分，并且认为独创性的高度和作品的保护程度密切相关，独创性高的作品，应当受到更强的保护。[2]不过，法院并没有给出判断独创性高低的统一指引，而是根据不同的案情发展出了多种不同的规则。如美国在实践中发展出了“抽象概括法”[3]“减除测试法”[4]以及“抽象-过滤-对比测试法”[5]等适用于不同种类作品的诸多判断规则。

不过，既然表达方式唯一或者有限则不具备独创性，那反过来说，如果表达方式有成千上万种，那就应当具有独创性。为此，一个简单的推论就是，在判断独创性大小的时候，其本质就是计算表达方式的具体数量。以最为常见的文学作品为例，本文认为，如果将其中最为基本的意思表达单元称之为“元素”，则该作品的表达方式数量就取决于作者选择了哪些元素、元素的排列方式以及各个元素具体的表达方式。下文将对此逐一进行阐述。

二、具体元素的筛选

具体元素的筛选属于最容易被公众所忽略的部分。读者所看到的是一部已经完成的作品，往往不会注意到作者在创作过程中对各种元素的取舍。作品好比是一座浮在水面上的冰山，大家看到的只有露出水面的那一小部分，隐藏在水底下的巨大冰体却很难引起大家的注意。

以文学作品中最常见的人物描写为例，其描述对象主要分为外貌、语言、动作和心理4大部分，其中外貌描写又可以分为容貌、神情、服饰、动作、形态等部分。在描写一个具体人物时，作者并不会涉及上述全部内容，而是会选择其中最能代表该人物的那些特性来展开描写。

假定外貌描写中共有20种不同的元素，而作者从中选择了10种。根据数学中的组合数理论，选择第一个元素时有20种选择，第二个元素为19种，依次类推，第10个元素为11种。在10个元素选定后，它们之间还有不同的排列顺序，但在此时先不用考虑，故还需要除以10个元素所有的可能的排列方式。在选出的这10个元素具体的排列数量上，第一位有10种可能，第二位有9种可能，依次类推，最后一位只有1种可能。综上，作者可以采用的元素组合为：

该数值的大小相信会让大部分读者大吃一惊，但计算结果就是如此。如果用数学符号来表示，就是“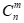”，其中C指的是组合数（(combinatorial number)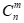），指的是从n个元素中选择出m个元素的所有组合的数量。

在元素的筛选过程中，有的时候会遇到必须被选上的“关系户”，也就是所谓的“必要场景”。必要场景指的是在描写到某个主题的时候必然会提到的内容，如描写文革的作品，往往都会提及上山下乡、忠字舞、红卫兵、大字报等元素。“关系户”的存在，会让作者选择元素的余地大为缩水。

在20个元素中选择10个，好比是20户居民参加10套房子的摇号。按照前面的计算方式，可能出现的结果共有184,756种，每户居民中签的概率都是50%。不过，如果其中5套房子被5个关系户内定，那结果就变成了15户“草民”争夺剩下的5个名额。此时，每个草民的中签概率降低到33.33%，可能出现的结果为变为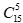，其值为3003，仅为原来的1.625%。这个结果也容易理解，此时关系户一个都不中，或者只中1~4个的情形都已经被排除，故最后结果的数量必然会显著下降。由于“必要场景”这个“关系户”并不影响表达的数量，故在著作权侵权案件中，会将属于必要场景的内容排除在外。

三、元素的排列顺序

在前文的分析中，我们并未考虑元素排列顺序的问题，但在作品中，元素的排列顺序也属于不可或缺的元素。在前文的例子中考虑排列顺序，那分母中的10的阶乘（用数学符号表示就是“10！”）就不必要扣除。根据数学计算可知，“1×2×3……×10”的结果是362.88万。

这个数字相信又会让很多人大跌眼镜，但数学结算的结果不容置疑。元素数量虽少，但只要排列的顺序够多，那最后的结果完全可以非常庞大。小时候我们玩的七巧板就是这样的一个例子。七巧板只有7块拼版，但由于排列的方式多种多样，故可以组合出成百上千种不同的图形。

在数学中，M个元素进行全排列的结果用“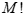”来表示。排序数量的数学规律也显示，元素数量只要有微小的变化，最后的结果会呈现指数级的放大。如果元素数量只有5个，则全排列的数量为120种；元素增加到10个，则为362.88万；加到20个，结果则高达2.433×1018，也就是243.3亿亿。中国的人口大致有13.86亿，如果将243.3亿亿元人民币平均分配给大家，则每人可以获得17.55亿元。就算是王健林这样的土豪，也足够完成17个小目标。

当然，在文学作品中，元素的排列顺序要受到语法限制，其结果远小于数学理论值。不过在符合语法的情况下，变换元素排列顺序而导致结果大相径庭也很常见。假定有这样一个场景：在楼梯口，某年轻人看到一位老大爷吃力的拎着一个箱子，于是上前帮忙。我们比较下年轻人这两句话的沟通效果：

（1）老大爷，东西我帮你拿。

（2）老东西，大爷我帮你拿。

前一句是助人为乐的社会主义好青年，后一句则变成了毫无教养的小流氓。在这两句话中，交换了“大爷”和“东西”的顺序，沟通效果完全不同。这就是元素排列顺序所带来的“威力”。

 又比如，大家对下面这道小学语文题应当都是耳熟能详：

 
题目要求

使用适当的连接词，将下列词语组合成一句句子：

 张姐姐、瘫痪、顽强学习、学会多门外语、学会针灸

标准答案

张姐姐虽然瘫痪了，但顽强地学习，不仅学会了多门外语，而且还学会了针灸。

脑洞大开的孩子则给出了下面这两个答案：

 （1）虽然张姐姐顽强学习，学会了针灸和多门外语，可她还是瘫痪了。

（2）张姐姐学会了外语，还学会了针灸，她顽强地学习，终于瘫痪了！

在变换了各个元素的顺序之后，句子所表达出来的意思截然不同。标准答案宣扬的是一位身残志坚的模范青年，而孩子们则将其恶搞成了学习过度而导致残疾的悲伤故事。

在文学作品中，这种排列顺序上的选择体现为情节结构、逻辑顺序等方面。在琼瑶诉于正案中，法院就明确指出，“文学作品中，情节的前后衔接、逻辑顺序将全部情节紧密贯穿为完整的个性化表达，这种足够具体的人物设置、情节结构、内在逻辑关系的有机结合体可以成为著作权法保护的表达。”[6]

四、元素本身的表达数量

元素本身的表达数量就是大家所熟悉的“思想表达二分法”中的表达，不过表达的数量所存在的内在规律也容易被大家忽视。以少女钟灵在《天龙八部》第一章中出场的描写为例，金庸先生给出的具体描述如下：

那少女约莫十六七岁年纪，一身青衫，笑靥如花，手中握着十来条尺许长小蛇。

在本描写中，大家没有必要去追究一些次要的细节。少女手中抓着十来条小蛇无疑会给人一种蛇发女妖美杜莎的既视感，画面太美不敢想象。我们只要注意到，这里的外貌描写涉及到了年龄、服饰、表情以及动作4个元素。

在这4个元素中，每个元素都存在多种可供选择的表达。在不改变原文主要信息的前提下，前述元素还可以表达为“二八年华”“一袭天青色衣衫”“笑意盈盈”以及“十来条尺许长小蛇在手中不停扭动”。假定每个元素都有20种表达方式，则4个元素的总表达方式就是“20×20×20×20”，共计16万种。事实上，如果是一个训练有素的写手，每个元素写出100中不同的表达方式也不在话下。

由于句子的表达数量为每个元素（Xi）表达数量连续相乘的积，用数学公式表示即为“”。即使每个元素的数量都很小，只要元素的数量足够多，那最后得到的结果也极为庞大。

以“全国专利代理人资格考试”为例，其卷一和卷二各为100道选择题。考虑到解析的内容受到题目的严格限制，故这里也假定每道真题仅存在2种解析。此时，100道真题的解析共存在2100种表达方式，也就是1.268×1030。

目前，全球人口总数为74亿，如果每人每秒钟发1万元人民币，则1.268×1030元人民币需要发5.432亿年。在5.432亿年前，地球处于寒武纪时期，正是三叶虫繁盛的时代，高等生命完全没个影儿。

如果我们有魄力一点，每人每秒钟发1亿元人民币，则需要发5.432万年。中国的历史也就上下五千年，五万年人类社会还处于旧石器时代末期，能够掌握的典型工具也就是梭镖。

另外需要强调的是，在实践中，表达方式的数量远比我们想象的要多，如以专利代理人资格考试2012年相关法第3题为例，其题目如下：

题目

根据民法通则及相关规定，下列哪种情形存在不当得利？

A、某地新建一公园，使得刘某在该公园周边的房屋大幅升值

B、银行工作人员因失误多给了孙某100元钱

C、赵某的朋友自愿替其偿还1万元债务

D、丁某在垃圾箱中捡到1台废弃的电脑

答案

兄弟我给出的解析为：

工作人员的失误属于不当得利。

从表面上看，似乎可以存在的解析也就一两种，但仅是在保留原有解析结构的前提下，对其中的各个元素进行适当的改变，可以轻易给出27（3×3×3）种不同的表达，如下表所示。

从该范例可以明显看出，表达方式的多样性远比我们想象的要多。如果是原封不动的复制，则很难逃脱侵权之责。当然，如果行为人对部分元素进行改写，则侵权的可能性就会显著下降。

作品的保护范围与其独创性相关，独创性越高的作品，受到的保护越高。在众多涉及到“创意与形式之争”的著作权侵权案件中，可以说“借鉴与剽窃，只在一线间”。[7]不过，如果是属于原封不动复制的“低级抄袭”，那试图通过主张涉案作品不具有独创性来进行抗辩恐怕很难成功。

五、独创性的数学计算模型

综合考虑前文提及的因素，计算表达独创性（Originality，下文简称为O）的数学公式就是：

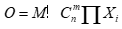
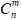其中，“”代表M个元素之间可能的全部排列顺序，“”代表不考虑元素排列顺序时，从n个元素中选择m个元素的组合数。“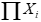”为连乘符号，代表将所有Xi进行连续相乘的积，即X1×X2×X3×X4×……Xm。考虑到具体案例中，有些元素的顺序是固定的，不能随意变动，M和m的值不一定相同，故本文不将“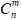”和“”合并为排列数（Array number）“”。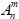

从上述公式可以明显看出，元素的数量每增加一个，对排列、组合以及表达这三个要素的数量都会产生影响，且“加速度”越来越大，最终形成类似铀元素裂变般的“链式反应”。

在侵权判断中，考虑的是双方在扣除公有领域的内容后，双方所余下的内容共同之处。如果某人抄袭了一个作者所独创的100处内容，则很容易构成侵权。不过，如果这100个内容来自于100个不同的作者，那情况就会发生实质性变化。作者不同，不能将独创性值相乘，故不容易构成侵权。为了织一件羊绒衫，从100只山羊身上各薅一把羊毛尚可接受，照着一只羊死命薅则是另外一回事。

综上所述，即使单个元素的独创性较低，但使用数量过多，导致在后作品成为在先作品的替代，无疑会损害在先作者的利益。单个元素的创新虽小，但不积跬步，无以至千里。

[1] 王迁：《知识产权法教程》，中国人民大学出版社2014年版，第28、33页。

[2] 如最高人民法院在《关于充分发挥知识产权审判职能作用推动社会主义文化大发展大繁荣和促进经济自主协调发展若干问题的意见》中明确指出，“要妥善处理作品的独创性与独创高度的关系，既维护给予作品著作权保护的基本标准的统一性，又注意把握各类作品的特点和适应相关保护领域的特殊需求，使保护强度与独创高度相协调。”

[3] Nichols v Universal pictures Corp. 45F. 2d 119 (2d Cir. 1930)

[4] Alexander v. Haley, 460 F. Supp. 40, 46 (S.D.N.Y 1978).

[5] Computer Associates International, Inc. v. Altai, Inc. 982 F.2d 693 (2d Cir. 1992).

[6] 北京市高级人民法院（2015）高民（知）终字第1039号民事判决书。

[7] 谭乃文：“借鉴与剽窃，只在一线间”，《民主与法制时报》2013年9月9日，第023版。

图片来源 | 图虫创意